Ponieważ wszechświat dyskursu X zbioru rozmytego składa się z rzeczywistej linii R, niepraktyczne byłoby wymienienie wszystkich par definiujących MF. Bardziej realnym sposobem zdefiniowania MF jest użycie wzoru matematycznego. Dwa z popularnych MF (trójkątne i trapezowe) stosowane w literaturze przedstawiono matematycznie za pomocą równań oraz na rysunku.
Definicja 2: Trójkątna MF Trójkątna MF jest definiowana przez trzy parametry (a, b i c) pokazane w poniższym równaniu:
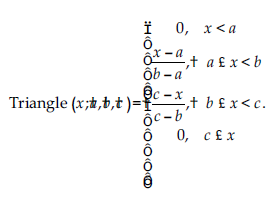
Parametry {a, b i c} (przy a <b <c) określają współrzędne x trzech rogów leżącego pod spodem trójkątnego MF.
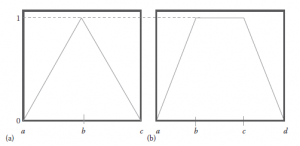
Definicja 3: Trapezoidalna MF Trójkątna MF jest definiowana przez cztery parametry (a, b, c i d), które są zapisane w postaci równania w następujący sposób:
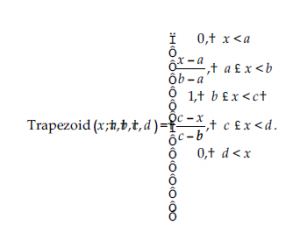
Ze względu na ich wydajność obliczeniową, oprócz prostych wzorów, trójkątne i trapezowe MF są szeroko stosowane w wielu implementacjach czasu rzeczywistego. Podstawowy FIS składa się z komponentów koncepcyjnych, które działają wspólnie, wykonując następujące trzy podstawowe kroki