Zaufanie jest szeroko interpretowane jako zależność między przekonaniami, w której jednostka jest przekonana, że inny partner będzie działał uczciwie lub zgodnie z jego przeznaczeniem. Jak wskazano większość prac dotyczących zarządzania zaufaniem w literaturze opiera się głównie na heurystyce i symulacji jako metodzie oceny i prawie żadna z nich nie jest wdrażana i testowana w rzeczywistym środowisku. Rozwiązania są często trudne do porównania, nawet na podstawie symulacji, ponieważ często opierają się na różnych hipotezach i są ukierunkowane na różne scenariusze zastosowań. Porównanie różnych metod jest zatem niezwykle trudne do wykonania, głównie z powodu dużego wysiłku symulacyjnego, który byłby wymagany. Modele szkła wirującego, takie jak słynny model Sherringtona-Kirckpatricka, już okazały się niezwykle wszechstronne i cenne w zrozumieniu globalnego zachowania złożonych systemów, takich jak sieci neuronowe, których dynamikę można modelować za pomocą mechaniki statystycznej Isinga o nieskończonym zasięgu. szklanki wirowe. W tej sekcji pokazano, w jaki sposób metody statystyczne mogą być również wykorzystywane do zrozumienia złożonej dynamiki, która wynika z lokalnych interakcji rówieśników w zdecentralizowanych sieciach, zgodnie z pracą Ermona i inych. Rozważmy sieć składającą się z N węzłów, reprezentowaną przez skierowany graf G = (V, E), w którym każda jednostka może komunikować się z pewnym podzbiorem innych węzłów zgodnie z macierzą sąsiedztwa A. Przedstawiony jest rzeczywisty stan wiarygodności każdego węzła i tak jak w przypadku zmiennej bitowej Ti Œ {—1,1}, abyśmy wspólnie opisali stan zaufania sieci za pomocą rzeczywistego wektora zaufania T {—1,1}N, przyjmując konwencję
W rzeczywistych warunkach pełny rzeczywisty wektor zaufania T jest nieznany rówieśnikom, a węzły są zwykle w stanie ocenić swoich sąsiadów na podstawie historii ich poprzednich interakcji, które są statystycznie skorelowane z rzeczywistym stan wiarygodności węzłów. Zakłada się, że T nie zmienia się w czasie i jest powiązane z macierzą opinii C RNxN za pomocą następującego równania:
C = f (T, w) w ( W)
gdzie:
Ω to przestrzeń próbna
f(·) reprezentuje sposób, w jaki powstają opinie
Każdy element cij macierzy opinii C to opinia, którą węzeł i ma na węźle j i zakładamy, że jest on istotny tylko wtedy, gdy i i j są sąsiadami, ponieważ opiera się na historii ich wcześniejszych interakcji. W tym modelu rolą algorytmu zarządzania zaufaniem jest szacowanie T z C, zakładając, że C i postać f(·) w równaniu są znane. Rolą algorytmu szacowania zaufania jest znalezienie konfiguracji zaufania 
które szacuje rzeczywisty wektor zaufania T. Podejście zastosowane tutaj polega na poszukiwaniu konfiguracji, która z większym prawdopodobieństwem wygenerowała pewną obserwowaną macierz opinii C, lub innymi słowy, konfigurację zaufania o najwyższym prawdopodobieństwie a posteriori 
LH (S; 
) dowolnej konfiguracji S, biorąc pod uwagę macierz opinii, C jest zilustrowane następującym równaniem:
gdzie:
jest prawdopodobieństwem T z warunkiem 
Zgodnie z regułą Bayesa,
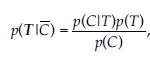
gdzie:
p(T) jest prawdopodobieństwem a priori dyskretnej zmiennej losowej T {-1,1}N p(C) i p(C|T) są gęstością i gęstością warunkową ciągłej zmiennej losowej C RNxN
Przyjrzyjmy się symetrycznemu zachowaniu wiarygodnych i niewiarygodnych węzłów. Jeśli p(T) jest symetryczne, wynikowa funkcja prawdopodobieństwa LH(T;C) staje się symetryczna w T, co jest sytuacją, w której skuteczne rozróżnienie między dwoma rodzajami węzłów byłoby wyraźnie niemożliwe. Dlatego skoncentrujemy się na rozkładach a priori rzeczywistego wektora zaufania p(T), które są niezrównoważone, to znaczy uprzywilejowują obecność jednego rodzaju węzła. Załóżmy, że rozkład prawdopodobieństwa a priori ma rozkład Bernoulliego z parametrem p, mianowicie
p : P(Ti = 1).
Następnie zakładając niezależność, jeśli zdefiniujemy w(T) = |{iIT = 1}|, otrzymamy:
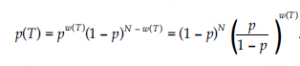
Ponieważ
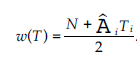
równanie powyższe staje się
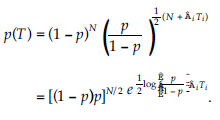
W ten sposób to uzyskaliśmy
gdzie:
γ normalizuje się do rozkładu prawdopodobieństwa
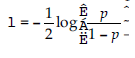
W przypadku, gdy rozkład a piori jest ukierunkowany na węzły godne zaufania lub odwrotnie dla λ = 0 (lub równoważnie p = 0,5), mamy przypadek symetryczny, w którym nie możemy oczekiwać dobrych wyników estymacji. Podsumowując, otrzymujemy:
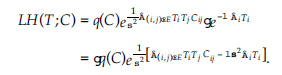
Dlatego z równania tego można łatwo wywnioskować, że prawdopodobieństwo LH(T;C) konfiguracji T jest proporcjonalne do monotonicznej funkcji rosnącej
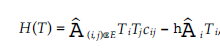
gdzie
η = σ2
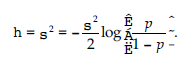
Dlatego możemy obliczyć oszacowanie maksymalnego prawdopodobieństwa rzeczywistego wektora zaufania, ustawiając i maksymalizując Równanie powyższe dla wszystkich możliwych konfiguracji T. Jest bardzo ważne, ponieważ reprezentuje energię lub hamiltonian konfiguracji S w modelu Isinga w obecności zewnętrznego pola magnetycznego o sile η, które łamie symetrię układu. Potwierdza to w przypadku symetrycznego rozkładu a priori T, czyli p – 0,5, pole magnetyczne zanika i układ staje się całkowicie symetryczny.