Reguła głosowania umożliwia wielokrotne ocenianie każdego węzła przez jego sąsiadów. W szczególności wyrażają swoje opinie poprzez głosowanie nad ich wiarygodnością, a zasada głosowania uwzględnia ich wraz z aktualnym szacowanym statusem wiarygodności uczestników głosowania. Aby naśladować algorytm Metropolisa-Hastingsa, wprowadzamy do reguły stochastyczność, dzięki czemu uzyskujemy pożądaną strukturę łańcucha Markowa z odpowiednim rozkładem prawdopodobieństwa stanu ustalonego. W każdym kroku czasowym węzeł i jest wybierany losowo. Wiarygodność Sj(k + 1) węzłów j, które są różne od i, są utrzymywane na stałym poziomie, podczas gdy, węzeł i przyjmuje następującą regułę głosowania do obliczania Si(k +1):
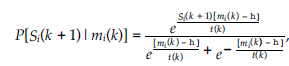
gdzie mi(k) definiuje się następująco:
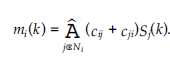
Ni to zbiór sąsiadów węzła i, a t(k) to parametr temperatury w iteracji k. W ten sposób łańcuch Markowa z przestrzenią stanów uzyskuje się jako [- 1, 1]N i z prawdopodobieństwem przejścia p[S,R]:= P[S(k +1) = R |S(k) – S], czyli równe zero, jeśli odległość Hamminga S i R jest większa niż 1. Jeśli odległość Hamminga S i R jest mniejsza lub równa 1, mamy to
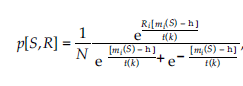
gdzie i jest indeksem takim, że Sj = Rj dla wszystkich j ≠ i
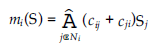
Ustalając parametr temperatury t w czasie, reguła głosowania jest po prostu zmodyfikowaną wersją klasycznego algorytmu Metropolisa-Hastingsa, w którym łańcuch Markowa ma różne prawdopodobieństwa przejścia, ale z tym samym rozkładem prawdopodobieństwa stanu ustalonego. Graf powiązany z łańcuchem Markowa jest silnie powiązany i składa się ze skończonej liczby (2N) stanów, z których każdy ma własną pętlę. Dlatego macierz przejść jest prymitywna, a wynikowy łańcuch jest regularny. Korzystając z twierdzenia Perrona-Frobeniusa, udowodniono, że istnieje unikalny rozkład prawdopodobieństwa w stanie ustalonym, który można uzyskać z dowolnego początkowego rozkładu prawdopodobieństwa. Dlatego wyciągnięto wniosek, że jeśli t = 1/β jest ustalone, to reguła głosowania definiuje łańcuch Markowa, którego rozkład prawdopodobieństwa stanu ustalonego π jest rozkładem Boltzmanna:
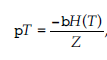
gdzie:
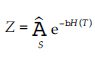
Wybór reguły głosowania nie jest jednak fundamentalny, ponieważ rozkład prawdopodobieństwa stanu ustalonego podany w Równaniu 8.26 można uzyskać przy użyciu standardowego Algorytmu Metropolisa, czyli wybierając następujące prawdopodobieństwo przejścia:
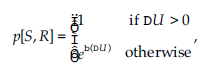
gdzie:
ΔU = 2Si[η – mi(S)]
S i R to stany z odległością Hamminga równą 1,
i jest takie, że Sj = Rj dla wszystkich j ≠ i oraz Si ≠ Ri
Z równań powyższyvh gwarantuje się, że powiązany łańcuch Markowa zbiegnie się do równania rozkładu Boltzmana, rozkładu prawdopodobieństwa w stanie ustalonym. Jednak współczynnik konwergencji zależy od wartości własnych macierzy przejścia, a tym samym od zastosowanej reguły głosowania.
Rola parametru β to współczynnik, który pozwala dostroić trudność problemu, który waha się od trywialnego przypadku, gdy β = 0 (wysoka temperatura)) i bardzo trudnego, jak β → ∞, a układ zamraża, koncentrując całą wagę na stanie podstawowym. W rzeczywistości, nawet jeśli użyjemy algorytmów do próbkowania takiego rozkładu prawdopodobieństwa dla dowolnej wartości β > 0, ich prędkość zbieżności jest określona przez wartości własne macierz przejścia do pożądanego rozkładu prawdopodobieństwa stanu ustalonego maleje wraz ze spadkiem temperatury.
Wynika to z faktu, że łańcuch Markowa jest ergodyczny dla każdej wartości β, ale stopień ergodyczności maleje jako β wzrasta, ponieważ ruch w dół staje się mniej prawdopodobny i dlatego łatwiej jest utknąć w lokalnych minimach H(S) Z drugiej strony, dla małych wartości β występuje szybsza zbieżność, ale wynikowy stały rozkład prawdopodobieństwa jest hałaśliwy z powodu rozkładu masy w wysokich temperaturach.) W tej sekcji, matematycznie poprawne ramy oceny zaufania w zdecentralizowanych sieciach autonomicznych Algorytm wykorzystuje podstawową właściwość polegającą na tym, że jest całkowicie oparty na lokalnych interakcjach między węzłami bez potrzeby centralnej koordynacji. Te lokalne interakcje charakteryzują się kilkoma poziomami losowości, obydwa są nieuniknione ze względu na niepewność co do opinii, że węzły mają swoich sąsiadów i sztucznie wprowadzone przez algorytm w regule głosowania. Wysoki stopień odporności algorytmu sprawia, że nadaje się on do różnych ustawień w sieciach rozproszonych, ponieważ zapewnia, że do pewnego stopnia system jest odporny na nieprawidłowe działanie lub nawet złośliwych użytkowników, którzy próbują zagrozić systemowi. W tej sekcji przedstawiono solidne matematycznie ramy oceny zaufania w przedstawione zdecentralizowane sieci autonomiczne. Algorytm wykorzystuje podstawową właściwość polegającą na tym, że jest całkowicie oparty na lokalnych interakcjach między węzłami, bez potrzeby centralnej koordynacji. Te lokalne interakcje charakteryzują się kilkoma poziomami losowości, z których oba są nieuniknione z powodu niepewności co do opinii węzłów o swoich sąsiadach i sztucznie wprowadzone przez algorytm w regule głosowania. Wysoki stopień niezawodności algorytmu sprawia, że nadaje się on do różnych ustawień w sieciach rozproszonych, ponieważ zapewnia, że do pewnego stopnia system jest odporny na nieprawidłowe działanie, a nawet złośliwych użytkowników, którzy próbują zagrozić systemowi.