Zaufanie w Cyberspace : Głosowanie ważone

Przedstawiamy prostą regułę oceny zwana prostą regułą głosowania do oceny wartości ufności. Załóżmy, że bezpośrednie wartości ufności są stałe, to znaczy za każdym razem τ ≥  0, c_it(τ) = c_ik, i nie zawsze jest to prawdą, ponieważ węzły zawsze są skłonne dostosować swoje opinie w oparciu o nowe informacje. Ta sekcja dotyczy konwergencji zasad oceny. Zmieniając wartości głosów, czas konwergencji będzie się różnił, ale ostatecznie wartość zaufania zbiegnie się do tego samego stanu ustalonego, biorąc pod uwagę, że opinie zostaną ostatecznie ustalone. t_ij(t) jest używane jako wartość zaufania i na j w czasie t .Wtedy

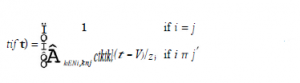
gdzie

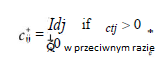
ponieważ brane są pod uwagę tylko opinie sąsiadów o pozytywnym przekonaniu, i

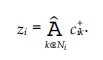
W regule głosowania węzeł k, sąsiad i, głosuje na cel j z bieżącą wartością zaufania, jaką ma t_kj(τ – 1) Węzeł i łączy wszystkie te głosy za pomocą średniej ważonej, gdzie wagi są równe bezpośrednim wartościom ufności i dla jego sąsiadów. Zwróć uwagę, że obliczenie f, y jest niezależne od wartości zaufania w innych węzłach. Jedyne wartości, które mają znaczenie, to wartości zaufania dotyczące j i bezpośrednie wartości zaufania. Oceńmy zaufanie w konkretnym węźle, powiedzmy na węźle 0. Zdefiniujmy macierz (N – 1) x (N – 1), c⁺⁰ = {c_tj^*}, i, j = 1 … N-1 i wektor zaufania na 0 jako T⁽⁰⁾ = [t₁₀, t₂₀ … ,t_(N-i)0] – Następnie przepisuje się pierwsze równanie  w formacie macierzowym w następujący sposób:

gdzie:

Z(0) = diag [z₁, …, z_N-1].

Powyższe równanie działa również dla oceny w innych węzłach. Równanie można wykorzystać, pomijając indeks 0, jak poniżej:

Gdy τ stanie się duży, wektor zaufania zbiegnie się do stanu ustalonego, który decyduje o wartościach zaufania w celu. Niech t_i0 = lim_τ→∞ t_i0(τ), oznacza wartość zaufania i na 0 w stanie ustalonym. Wartości zaufania w stanie ustalonym nazywane są ostatecznymi wartościami zaufania, a te w dowolnym momencie przed konwergencją nazywane są tymczasowymi wartościami zaufania. Do ostatecznych wartości zaufania stosuje się regułę progową. Reguła progowa jest definiowana za pomocą parametrów η^– i  η⁺ w taki sposób, że wartość zaufania jest neutralna między η^– i  η⁺, podczas gdy warunek zaufania przeważa, gdy 1> wartość zaufania >  η⁺, a warunek braku zaufania występuje, gdy η^–   < wartość zaufania <-1.