W części „Analiza protokołów GKA dotyczących częściowej tajności przekazywania” przedstawiono analizę zestawu testowego protokołów przy założeniu jednolitego prawdopodobieństwa kompromitacji wszystkich kluczy i silnych uszkodzeń. Rozważmy BD, JV, BW, STW, KPT i KLL, protokoły w zestawie testowym, które są oparte na prymitywach kryptograficznych DH. Wykres prawdopodobieństwa złamania klucza sesji w stosunku do liczby uczestników (8–100) dla różnych protokołów i danego prawdopodobieństwa pokazano na rysunku .
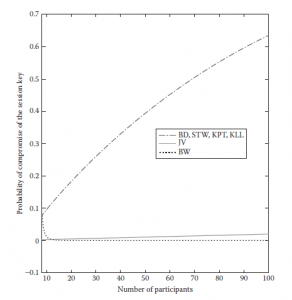
Maksymalny zakres n jest wybierany na podstawie typowej liczby uczestników aplikacji P2P, która wynosi 100. Działki wskazują na DPFS, czyli tajność kluczy sesyjnych dla większej liczby uczestników. Jako minimum przyjęto ośmiu, tak aby w grupie był co najmniej jeden członek pod każdym z czterech liderów protokołu BW. Zakłada się, że prawdopodobieństwo ujawnienia tajemnic (p) wynosi 0,01 dla wszystkich protokołów. Można zauważyć, że protokoły BD, STW, KPT i KLL wykazują podobną siłę w odniesieniu do częściowej poufności przekazywania przy założeniu jednolitego prawdopodobieństwa. Wartość DPFS dla tych protokołów jest wyższa w porównaniu z wartością JV i BW, co wskazuje, że są one słabsze niż JV i BW. Dla większych wartości n, BW ma najmniejszą wartość dla DPFS, wskazującą, że BW jest silniejszy niż JV. Rozważ protokoły BN, IDBP i A-GDH.2, każdy protokół w tym zestawie używa protokołu inny prymityw kryptograficzny. Wykres DPFS w porównaniu z liczbą użytkowników pokazany na rysunku
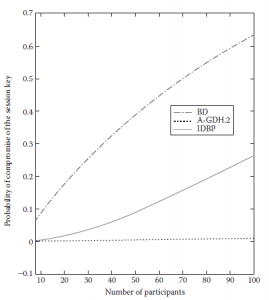
pokazuje, że protokół A-GDH.2 ma najniższą wartość DPFS i dlatego jest najsilniejszy, a następnie protokoły IDBP i BN, przy założeniu jednolitego prawdopodobieństwa kompromisu warunków . Analiza pokazuje, że struktura umożliwia porównanie protokołów wykorzystujących różne prymitywy kryptograficzne. Zaproponowana analiza i ramy otwierają drogę do sformalizowania koncepcji zaufania w aplikacjach grupowych. Zaufanie dotyczy wiary członka w bezpieczeństwo jego informacji lub transakcji w rękach innych członków grupy. Dlatego prawdopodobieństwo utraty tajemnic jest logicznym paradygmatem obliczeniowym, który należy przyjąć lub przypisać zaufanie. W następnej sekcji przedstawiono propozycję modelu zaufania dla komunikacji P2P i wyjaśniono ją na podstawie trzech przykładowych aplikacji. Zilustrowano również sposób, w jaki model zaufania mógłby być używany przez użytkowników tych aplikacji do podejmowania decyzji.