Systemy zaufania to systemy ratingowe, w których każda osoba jest proszona o wyrażenie opinii po zakończeniu każdej interakcji w formie ocen (może być ona dorozumiana lub jawna). W naszej pracy wartości zaufania i nieufności są wywnioskowane z bazy danych ratingów RS, a następnie wartości te są wykorzystywane w celu zwiększenia dokładności procesu rekomendacji. Te interakcje składają się z argumentów i zaleceń generowanych przez agentów. Argumenty są ważne dla wyjaśnienia wszelkiego rodzaju interakcji między agentami. Poprawia to jakość i użyteczność rekomendacji iteracyjnie w kilku cyklach [6]. Podczas argumentacji agenci mogą wcześniej uzgodnić lub nie zgodzić się w pewnych kwestiach; na koniec użytkownik akceptuje lub odrzuca rekomendację. Uważamy, że cokolwiek może być ostatecznym wynikiem procesu rekomendacji, zawsze odpowiadają za to różne argumenty (za lub przeciw). Dzieje się tak, ponieważ te argumenty stanowią podstawę generowanych rekomendacji. Dlatego ważne jest, aby oprócz zaleceń określić odpowiedzi agentów na takie argumenty. Zgoda i akceptacja określiłyby dokładniejszą wartość zaufania dla agentów w systemie, podczas gdy brak zgody i odrzucenie mogą jednocześnie określić nieufność w systemie. Również z perspektywy badawczej powszechnie uznaje się, że nieufność odgrywa ważną rolę, ale w tej dziedzinie pozostaje jeszcze wiele do zrobienia. Jak wspomniano powyżej, obliczyliśmy wartości zaufania i nieufności oddzielnie na podstawie interakcji agentów w systemie. Ale jak omówiono wszystkie podejścia , które traktują zaufanie i nieufność, jak dotąd, nie były w stanie osiągnąć konsensusu co do sposobu szerzenia nieufności. Różne operatory dają różne wyniki w zależności od interpretacji, dlatego bardzo ważny jest wybór odpowiedniego schematu rozmnażania dla danego zastosowania. W naszym przypadku, ponieważ proponujemy uogólniony model zaufania – nieufności dla każdego wniosku o rekomendację, w którym propagujemy i agregujemy wszystkie wartości zaufania – nieufności za pomocą rozumowania to ostateczna sugerowana wartość zaufania poprzez odjęcie ważonej rozmytej wartości zaufania od ważonej rozmytej wartości zaufania. Guha i inni poparli również łączenie wartości zaufania i nieufności ze względu na podobne problemy związane z propagowaniem nieufności, ale nie rozważali rozmytych środków w celu dalszej poprawy dokładności. Bardziej formalnie, niech A = {a1, a2,…,aM} to zbiór wszystkich agentów (zarówno użytkowników, jak i agentów rekomendujących), gdzie M to liczba agentów w systemie. Zakładamy, że każdy klient użytkownika oceni agenta rekomendującego po zakończeniu procesu rekomendacji. Interakcja i ∈ I, gdzie rxy(ik) jest oceną, którą agent x przyznał agentowi y za interakcję ik. Skala ocen lub ocena interakcji jest definiowana jako G = {−2, −1, 0, +1, +2}. Zbiór ocen, które agent x nadał agentowi y, to Sxy = {rxy(ik) | ik ∈ I} a cała przeszła historia agenta x to Hx = {Sxy | ∀ y(≠x) ∈ A}. Ocena agenta dla rekomendacji lub argumentu „ik” jest szacowana niejawnie na podstawie liczby dopasowań parametrów argumentu, które trafiają na listę preferencji agenta. Ocena może być również nadana bezpośrednio przez użytkownika na skali „G”, jak wspomniano powyżej. Biorąc pod uwagę, że A jest zbiorem agentów. Wiarygodność agenta definiujemy następująco: Trusts: A ¥ A ¥ F Æ [0,1]. Ta funkcja przypisuje każdemu agentowi rekomendującemu rozmytą miarę reprezentującą jego wiarygodność według innych programów użytkownika. Aby obliczyć wiarygodność agenta y (oznaczonego jako y), agent x (oznaczony jako x) wykorzystuje historię swoich interakcji (zarówno argumenty, jak i zalecenia) z y.

Tutaj Trustsxy oznacza ostateczną wiarygodność y zgodnie z punktem widzenia x. T_N_Argxy to łączna liczba argumentów przedstawionych przez y w stosunku do x, liczba utrzymywana przez trwałą bazę przekonań agenta w systemie. T_N_Rxy to całkowita liczba zaleceń wydanych przez y dla x, liczba utrzymywana przez trwałą bazę przekonań agenta w systemie. ÂArgOEIFM_agree (Argxy) jest sumą rozmytej miary stopnia zgodności x względem argumentów y, które są do przyjęcia dla x, otrzymanej z równania. ÂArgOEIFM_disagree(Argxy) jest sumą rozmytej miary stopnia niezgodności x argumentów y, które są nie do przyjęcia dla x, otrzymanej z równania. ÂROEIFM(Rxy)*vsatisfied jest sumą rozmytej miary stopnia spełnienia x względem zaleceń y uzyskanych z równań. Stąd te zalecenia są akceptowalne dla x. ÂROEIFM(Rxy)*vunsatisfied jest sumą rozmytej miary stopnia niezadowolenia x z zaleceń y uzyskanych z równania .Dlatego te zalecenia są nie do przyjęcia dla x. Tutaj vsatisfied i vunsatisfied to wartości (wagi) przypisane do akceptowalnych i niedopuszczalne argumenty rekomendacji. Teraz musimy znaleźć satysfakcję użytkownika (w jakim stopniu) i niezadowolenie (w jakim stopniu) z rekomendacji lub argumentu wygenerowanego przez agenta. Aby to zrobić, możemy zdefiniować dwa rozmyte podzbiory w ocenach każdego agenta, powiedzmy zadowolony i niezadowolony. Dzieje się tak, ponieważ zbiory rozmyte mogą jasno uchwycić koncepcję znalezienia zakresu (wartości członkostwa), w jakim agent jest zadowolony lub niezadowolony z interakcji. Zadowolone i niezadowolone rozmyte podzbiory dla x są zdefiniowane w następujący sposób:

gdzie:
satx(ik) i unsatx(ik) dają nam wyraźne wartości członkostwa dla ocen x po interakcji ik (argumenty i rekomendacje) w rozmytych podzbiorach, odpowiednio, spełnione (x) i niezadowolone (x)
Następnie określamy Rozmyte wartości członkostwa typu 2 dla ocen x w interakcji ik przy użyciu dwóch powyższych równań .

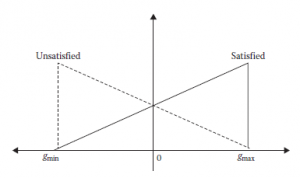
Teraz podajemy prostą trójkątną funkcję przynależności dla spełnionych (x) i niezadowolonych (x) rozmytych podzbiorów typu 1, które są zdefiniowane za pomocą następujących popularnych równań

gdzie :
gmin i gmax to minimalne i maksymalne oceny dla danego systemu, przy czym G = {gmin,. . ., 0,. . ., gmax} Aby rozmyć wartość funkcji przynależności uzyskaną z równania 14.4, używamy zestawów rozmytych przedziału typu 2 do uogólnienia zbiorów rozmytych typu 1. W ten sposób można poradzić sobie z większą niepewnością. Stąd teraz satx(ik)Œ{satx(ik)2, √satx(ik)} for zamiast być równą wartości liczbowej rxyik) – gmin gmax – gmin. To daje nam teraz elastyczność w definiowaniu poziomu satysfakcji użytkownika (zasięgu) przy użyciu rozmytych zbiorów typu 2 interwału. Uważamy, że różni użytkownicy (np. Stary, częsty i nowy użytkownik) mogą mieć różne poziomy zadowolenia z danego wyjścia. Częsty użytkownik oczekuje od systemu bardziej trafnych rekomendacji niż nowy użytkownik lub użytkownik, który rzadziej korzysta z systemu. Powiedzmy, że mamy trzy grupy poziomu satysfakcji (mniej zadowolony, umiarkowanie zadowolony i bardzo zadowolony). Tak więc zakres poziomu satysfakcji może się różnić w zależności od nowego użytkownika i częstego użytkownika, biorąc pod uwagę ten sam zestaw zaleceń. Ponadto stopień zadowolenia użytkownika (biorąc pod uwagę doświadczenie w użytkowaniu systemu) można określić jako:
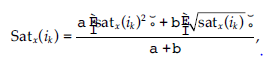
gdzie:
α i β są wagami przypisanymi do dolnej i górnej granicy przedziału rozmytego zestawu przynależności typu 2 {satx(ik)2, √satx(ik)} dla satx(ik), odpowiednio Tutaj α i β przyjmą wartości w trakcie wykonywania, zgodnie z typem użytkownika zalogowanego do systemu i potrzebującego zaleceń. Korzystając z Równania otrzymujemy
Unsatx(ik) = 1 – satx(ik).
Zbiory i systemy rozmyte typu 2 uogólniają zbiory i systemy rozmyte typu 1, dzięki czemu można obsłużyć większą niepewność. Funkcja przynależności zbioru rozmytego typu 1 nie jest związana z żadną niepewnością. Zbiór rozmyty typu 2 pozwala nam włączyć niepewność dotyczącą funkcji przynależności do teorii zbiorów rozmytych i jest sposobem na odniesienie się do powyższej krytyki zbiorów rozmytych typu 1. A jeśli nie ma niepewności, to zbiór rozmyty typu 2 redukuje się do zbioru rozmytego typu 1, co jest analogiczne do redukcji prawdopodobieństwa do determinizmu, gdy znika nieprzewidywalność. Na przykład w studium przypadku reprezentujemy przynależność do preferencji kosztowej produktu przez rozmyty zbiór przedziałów typu 2, to znaczy przynależność do kosztu dla każdego produktu w każdej kategorii, to znaczy niski, średni lub wysoki jest interwałem, a nie wartością wyraźną. W ten sposób można obsłużyć większą niepewność przy użyciu zbiorów rozmytych typu 2 niż przy użyciu zbiorów rozmytych typu 1. Poziom satysfakcji użytkownika można również zdefiniować za pomocą zbiorów rozmytych typu 2. Jak wyjaśniono powyżej, różni użytkownicy (dawni często i nowi użytkownicy) mogą mieć różny poziom zadowolenia z wygenerowanych zaleceń. Częsty użytkownik oczekuje od systemu bardziej trafnych rekomendacji niż nowy użytkownik lub użytkownik, który rzadziej korzysta z systemu. Dlatego zakres poziomów satysfakcji będzie różny dla nowych użytkowników i dla częstych użytkowników. Następnie, dla argumentacji między agentami w RS, definiujemy dwie kombinacje podzbiorów rozmytych zadowolonych i niezadowolonych, tj. Zadowolony – zadowolony zapisany jako SS (x, y) i niezadowolony – zadowolony zapisany jako US (x, y). Zakładamy, że x reprezentuje użytkownika, podczas gdy y reprezentuje osobę polecającą. Dlatego w przypadku rozmytego systemu zaufania ratingowego wartości zgodności i braku zgody w przypadku argumentu między dowolnymi dwoma agentami x i y są podane przez

Literatura dotycząca zbiorów rozmytych opisuje wiele alternatyw dla sumowania i przecinania zbiorów wyrazistych. Popularny to minimum dla skrzyżowania i maksimum dla związku. Alternatywa min – max i definicja liczności zbioru rozmytego dają następujące wyniki

Wszystkie te argumenty i zalecenia dotyczą konkretnej domeny. Podstawową ideą jest to, że poziom zaufania i nieufności agenta można oszacować na podstawie tego, ile informacji uzyskanych od niego zostało odpowiednio zaakceptowanych lub odrzuconych jako wiara w przeszłość.