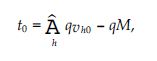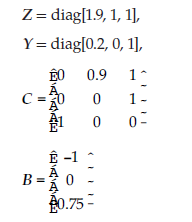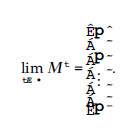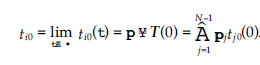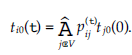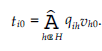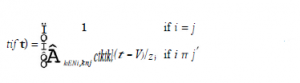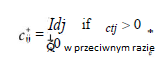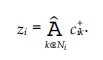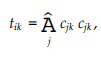Miesiąc: luty 2022

W tej sekcji opiszemy liniowe kodowanie sieci , które zapewnia wydajną propagację poświadczeń zaufania i powiązane operacje, które są zdecentralizowane. Kodowanie sieci to nowa dziedzina teorii informacji, której zaproponowano w celu poprawy wykorzystania przepustowości danej topologii sieci. Ahlswede i inni jako pierwsi wprowadzili kodowanie sieciowe. Przedstawmy powierników, którzy są zainteresowani wiarygodnością konkretnego użytkownika zwanego powiernikiem. Poświadczenia zaufania dotyczące powiernika są początkowo przechowywane w rozproszonych węzłach w całej sieci. Węzły te wystawiają poświadczenia zaufania lub pobierają je od innych. Poświadczenia zaufania będą wskazywać tylko jednego powiernika, a wszystkie operacje są stosowane na tych poświadczeniach dotyczących powiernika. Każde poświadczenie zaufania, w postaci dokumentu cyfrowego, ma unikalny identyfikator, który uzyskuje się poprzez zastosowanie funkcji skrótu do dokumentu. W sieciach autonomicznych węzły komunikują się bezpośrednio tylko z niewielkim podzbiorem innych węzłów zwanych sąsiedztwem, a węzły często sprawdzają u swoich sąsiadów nowe poświadczenia. Nowe poświadczenia są przekazywane do węzła, gdy wykryje je w swoim sąsiedztwie. Za każdym razem, gdy węzeł przekazuje dalej poświadczenia zaufania, tworzy liniową kombinację wszystkich poświadczeń, które ma obecnie w pamięci, i połączonych dokumentów, które otrzymał od sąsiadów.

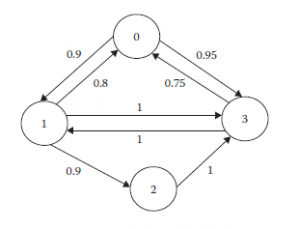
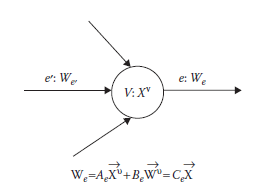
Rozważmy sieć jako graf G = (V, E), gdzie V to zbiór węzłów, a E to zbiór krawędzi. Krawędzie są oznaczone przez e – (v, v’)  E, gdzie v = head(e) i v’ =  tail(e). Zbiór nadchodzących krawędzi jest oznaczony jako I(v) = {e   E: head (e) = v}, a stopień wejściowy v to deg₁(v) =  |I (v)|. Podobnie zbiór  wychodzących krawędzi jest oznaczony jako O(v) = {e  E: tail (e) = v}, a stopień wyjściowy v to deg₀ (v) = |O(v)|. Oznaczmy przez X^v_l ,l= 1, … , h jedno z h poświadczeń, które przechowuje węzeł v, a przez W^v_e’, połączony dokument przesłany do v przez krawędź e’. Rozważ jedną wychodzącą krawędź v, krawędź e. Połączony dokument przesyłany za pośrednictwem łącza e jest zdefiniowany następująco:

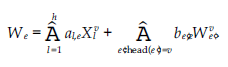
Wszystkie te operacje mają miejsce w skończonym polu F_q. Współczynniki a_l,e i b_e’e są wybierane losowo z F_q, a zawartość danych każdego dokumentu zaufania jest reprezentowana przez d elementy z F_q. Wektor współczynnika połączonego dokumentu  W_e jest definiowany jako C_e = [c_e,1, c_e,2r …, c_e,m], gdzie m to całkowita liczba dostępnych poświadczeń zaufania. Zgodnie z równaniem powyzej, współczynnik referencji X^l_v to a_l,e. Załóżmy, że współczynnik referencji X_l’ w połączonym dokumencie W^e_v wynosi c_e’l Wtedy mamy to

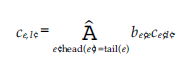
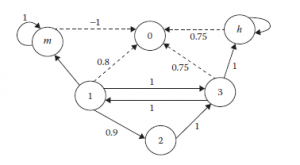
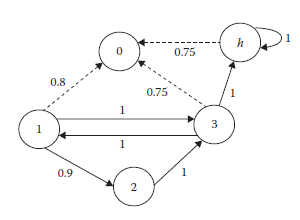
Rysunek przedstawia przepływ dokumentów od krawędzi e’ do węzła v i dalej do krawędzi e

Obserwuje się, że mając m różnych dokumentów zaufania, węzeł może je odzyskać po odebraniu m połączonych dokumentów, dla których powiązane wektory współczynników są od siebie liniowo niezależne. Proces rekonstrukcji jest podobny do rozwiązywania równań liniowych. Schemat oparty na kodowaniu sieci obejmuje tylko interakcje lokalne. Węzły nie muszą być świadome istnienia jakichkolwiek poświadczeń zaufania i ich lokalizacji. Kontaktują się tylko z sąsiadami, aby sprawdzić, czy są nowe poświadczenia lub nowe połączone dokumenty. Jest to zaleta w porównaniu z jakimkolwiek schematem żądanie-odpowiedź, takim jak schemat oparty na Freenet [30]. Schematy odpowiedzi na żądania wymagają tablic routingu. Jeśli topologia sieci zmienia się, gdy nowe węzły wchodzą do sieci lub niektóre węzły się przenoszą, tablice routingu należy natychmiast zaktualizować. Schemat kodowania sieci szybko dostosowuje się do zmian topologii, ponieważ węzły kontaktują się tylko ze swoimi obecnymi sąsiadami. Ponadto schematy żądanie-odpowiedź wymagają, aby węzły znały identyfikatory dokumentów przed wysłaniem żądań, co wymaga globalnej wymiany informacji. Schemat kodowania sieciowego działa bez znajomości identyfikatora dokumentu.

Sieci autonomiczne to sieci samoorganizujące się, kontrolowane i zarządzane w sposób zdecentralizowany. Relacje zaufania między sąsiadami są niezbędne, aby zapewnić, że transmitowane wiadomości nie przedostaną się do wroga. Ze względu na mobilność i dynamikę sieci autonomicznych często wymaga aktualizacji wartości zaufania. Ponadto ważność danych uwierzytelniających zaufania zmienia się wraz z upływem czasu oraz warunkami środowiskowymi. W związku z tym ustanawianie i utrzymywanie zaufania w sieciach autonomicznych jest znacznie bardziej dynamicznym problemem niż w tradycyjnych sieciach serwerowych. W sieciach autonomicznych poświadczenia zaufania są zwykle wystawiane i często przechowywane w sposób rozproszony. Scentralizowane zarządzanie zaufaniem, w którym wszystkie poświadczenia są przechowywane w jednej lokalizacji, jest zawodne. W przypadku trybu zdecentralizowanego dystrybucja poświadczeń rodzi wiele interesujących pytań, takich jak najlepsze miejsca do przechowywania danych uwierzytelniających, aby można je było łatwo zlokalizować, dobrze chronić i szybko dostrzec.

Po uzyskaniu przez użytkownika niezbędnych danych uwierzytelniających zaufania dla użytkownika docelowego, stosuje politykę oceny, aby wyciągnąć wnioski dotyczące wiarygodności użytkownika docelowego. Opracowano i przeanalizowano różne zasady. Chociaż wybór odpowiedniego modelu oceny zaufania i uzyskanie poświadczeń do obliczenia zaufania idą w parze, dystrybucja danych uwierzytelniających zaufania jest dość niezależna od konkretnego modelu oceny. Poświadczenia zaufania są wyświetlane jako pliki do udostępnienia w celu zarządzania zaufaniem. Problem dystrybucji danych uwierzytelniających zaufania wywodzi się z wielu cech rozproszonych systemów wymiany plików peer-to-peer (P2P), Jiang i Baras zaproponowali schemat dystrybucji danych uwierzytelniających zaufania, który wykorzystuje metodę liniową  kodowania sieciowego w celu łączenia danych uwierzytelniających podczas transmisji. W proponowanym zdecentralizowanym schemacie zastosowano podejście typu żądanie-odpowiedź, które skutecznie rozwiązuje dynamiczny charakter problemu. Schemat zwany kodowaniem sieciowym został również wykorzystany w udostępnianiu plików P2P. Gkantsidis zaprojektował system wymiany plików P2P o nazwie Avalanche, w którym rówieśnicy pośredniczący tworzą liniowe kombinacje bloków plików, jak w przypadku kodowania sieciowego. Acedanski przeanalizował pamięć masową opartą na losowym kodowaniu liniowym. Różne konteksty zaufania wymagają różnych typów poświadczeń, takich jak certyfikat cyfrowy i zintegrowany system automatycznej identyfikacji odcisków palców (IAFIS). Certyfikat cyfrowy jest wydawany przez urząd certyfikacji lub jednostkę i weryfikuje, czy klucz publiczny jest własnością określonej jednostki. Certyfikaty cyfrowe służą do udaremniania prób zastąpienia klucza jednej osoby innym. Certyfikaty cyfrowe są szeroko stosowane w PGP i X.509. IAFIS używa ludzkich odcisków palców jako tożsamości. Wartość zaufania określa stopień zaufania, jakim wystawca poświadczeń darzy użytkownika docelowego. Wartość może być binarna, zaufana lub nieufna, lub wielowartościowa, na przykład cztery poziomy zaufania do PGP , lub nawet ciągła w przedziale, powiedzmy [-1,1]. Poświadczenia zmieniają się w czasie i przestrzeni. Każdy użytkownik ma wartości zaufania dotyczące przechowywanych danych uwierzytelniających. Wartość ufności zależy od kilku czynników, takich jak czas, jaki upłynął od wydania poświadczenia lub odległość komunikacyjna, jaką poświadczenie zajęło, aby dotrzeć do użytkownika. Gdy wartość ufności jest poniżej określonego progu, odpowiednie poświadczenie uważa się za nieważne.

Teraz rozważamy więcej niż jednego, powiedzmy M, przeciwników jest obecnych w sieci. Zgodnie z założeniami przeciwnicy ci znają się nawzajem i potrafią zmowy, aby maksymalnie zniszczyć schemat głosowania. Podobnie, jak w powyższym argumencie, najgorszą strategią tych przeciwników M jest zawsze głosowanie – 1 na dobre węzły i odwrotnie 1 na innych przeciwników i nigdy nie zmieniają swoich głosów. Zatem w dwuznakach przeciwnicy są modelowani jako stany absorbujące. Załóżmy, że system ocenia dobry węzeł, powiedzmy 0. Załóżmy, że istnieją nagłówki H, a ich głosy w węźle 0 są oznaczone przez vh0 dla dowolnego nagłówka h. Jeśli przyjmiemy, że wykres zaufania jest idealnie regularny w tym sensie, że prawdopodobieństwa absorpcji nagłówków i przeciwników są takie same i są oznaczone jako q , a następnie q(H + M) = 1. Wartość zaufania określa następujące równanie:

co jest takie samo dla wszystkich węzłów oceniających. Następnie należy oszacować wpływ na bezpieczeństwo jako funkcję liczby przeciwników. Zgodnie z regułą progową, węzeł 0 nie jest zaufany, jeśli t < η⁺ i mamy q(S_hvho -M) < h⁺.

Zatem jeśli liczba przeciwników M > (S_hvho – h^*H)/(1+h⁺) = M^* schemat nie jest w stanie ocenić wiarygodności węzła 0. Dlatego M^* jest progiem odporności na atak dla schematu głosowania. W bardziej realistycznym scenariuszu jednostki o niskich wartościach ufności są łatwe do oszukania przez przeciwników. Adwersarze, którzy łączą się z podmiotami o niskim zaufaniu, mają mniejsze prawdopodobieństwo absorpcji, wtedy próg odporności na atak jest w rzeczywistości większy niż M^*, co oznacza, że ​​schemat jest odporny na więcej przeciwników. Argumenty dotyczące wykrywania przeciwników są podobne do oceny, z tym wyjątkiem, że liczba przeciwników jako stanów absorbujących wynosi (M – 1) zamiast M, ponieważ przeciwnik M-ty jest teraz celem oceny. W tej sekcji formalnie zdefiniowano strategię ustanawiania zaufania opartą wyłącznie na lokalnych interakcjach. Wprowadził również nowe pojęcie nagłówków, które pomagają w tworzeniu rozproszonego zaufania. Zachowanie zbieżności schematu wykorzystującego teorię grafów algebraicznych jest badane i interpretowane jako łańcuch Markowa na dwuznaku. Ponadto omówiono wpływ topologii na rozprzestrzenianie zaufania, co wyjaśnia nowy sposób zarządzania siecią. Ponieważ zarządzanie zaufaniem jest ważnym elementem bezpieczeństwa sieci, badane są kwestie dotyczące ustanowienia zaufania w obecności adwersarzy.

W rozproszonym ustanowieniu zaufania przeciwnik bierze również udział w ocenie innych węzłów. Ponieważ stosuje się nieufność w jednym kroku, nikt nie weźmie pod uwagę opinii przeciwnika. Przeciwnik nie może nic zrobić dla oceny zaufania. To właściwie jedna z zalet jednostopniowego modelu nieufności. Jednak w scenariuszu rozproszonym przeciwnik może oszukiwać, aby zdobyć zaufanie niektórych dobrych węzłów; wtedy głosy dostarczone przez przeciwnika są również propagowane w sieci. Celem przeciwników jest maksymalne obniżenie wartości zaufania celu poprzez wybór strategii głosowania i oceny. Zakładamy, że przeciwnik stosuje najgorszą strategię, która minimalizuje wartość zaufania: zawsze głosuje – 1 na dobre węzły i nigdy nie zmienia głosów. Biorąc pod uwagę łańcuch Markowa, przeciwnik korzystający ze strategii najgorszego przypadku jest również modelowany jako nagłówek z vm0 = -1. Rysunek  przedstawia przykład, w którym node1 błędnie ufa złośliwemu węzłowi m z wartością ufności 0,2. Jeśli wartość zaufania jest obliczana przy użyciu równania  T = (Z + Y – C )^-1YB przy

Następnie mamy T = [0,45, 0,60, 0,60] ‘w porównaniu z oryginalnym T = [0,75, 0,75, 0,75]’ bez złośliwego węzła.

Aby ocenić dany węzeł, opinie o zaufaniu rozpoczynają się od węzłów, które mają bezpośrednie relacje zaufania z celem. Opinie te rozprzestrzeniają się po całej sieci i ostatecznie docierają do wszystkich węzłów w sieci. Rozważmy teraz konwergencję systemu, a także zbadajmy rozprzestrzenianie się zaufania, gdy system osiąga stan ustalony. Rozważmy sieć cnotliwą bez przeciwników, w której wszystkie węzły zachowują się racjonalnie, to znaczy wszystkie węzły stosują się do wstępnie zaprojektowanej reguły oceny, a ten przypadek skutkuje C⁺ = C. Analiza przedstawiona poniżej pokazuje, że zaufania nie można ustanowić za pomocą prostej reguły głosowania. Zdefiniuj macierz M = Z^-1C. Następnie równanie 8.6 aktualizacji stanu można zapisać w następujący sposób:

T(t) = MT(t-1) = M^TT(0)

M można postrzegać jako ważoną macierz sąsiedztwa wykresu zaufania. Konieczne jest sprawdzenie, czy M jest matrycą stochastyczną. Macierz nazywana jest macierzą stochastyczną, jeśli suma elementów każdego wiersza wynosi 1. Ponieważ M jest macierzą stochastyczną, największa wartość własna Mis 1. Mówi się, że graf zaufania jest silnie połączony, jeśli do każdego węzła można dotrzeć z każdego innego węzła podążającego za kierunkiem krawędzi. Można wykazać, że wykres, którego (ważona) macierz sąsiedztwa jest M, jest silnie powiązany wtedy i tylko wtedy, gdy macierz jest błędnie nieredukowalna. Niech wektor wierszowy π będzie lewym wektorem własnym (wektorem wierszowym) odpowiadającym wartości własnej 1 z |π| = 1, a następnie πM = π. Można to udowodnić przez ergodyczność, która mówi

Zatem i, 1 ≤ i  ≤ N -1

Ponieważ t_i0 jest niezależne od i, każdy węzeł osiąga tę samą wartość zaufania w stanie ustalonym. Jak widać, wartości zaufania zależą wyłącznie od początkowego wektora zaufania T (0). Jeśli węzeł jest na początku zaufany przez dużą część węzłów w sieci, jego wartości zaufania są wysokie w stanie ustalonym. Jednak w sieciach rozproszonych początkowo tylko niewielka liczba węzłów ma bezpośrednie relacje zaufania z celem, to znaczy T (0) jest rzadki i zawiera kilka niezerowych wpisów. Ponadto wpisy n są zwykle małe, gdy N jest duże. Na przykład rozważmy wykres regularny / c, na którym wszystkie łuki mają wartość ufności 1. Następnie lewy wektor własny p = [1 /(N -1), …, 1 /N -1)]^¢ Ponieważ wykres zaufania jest rzadki, k << N, mamy

t_i0 = k /N – 1 << 1

Wynik wskazuje, że nawet w sieci, w której wartości ufności wszystkich sąsiadów są równe 1, wartości zaufania w stanie ustalonym są bardzo małe, to znaczy bliskie 0. W związku z tym, zgodnie z prostą regułą głosowania, ustanowienie zaufania jest prawie niemożliwe, nawet jeśli wszystkie wartości głosów to 1. W celu przezwyciężenia tego problemu wprowadza się nagłówki, które są wstępnie zaufanymi podmiotami o wartości zaufania 1. Jednostkę można uznać za nagłówek tylko wtedy, gdy udowodniono, że jest niezawodna i odporna na ataki. Zdefiniujmy liczbę nagłówków i, którym ufam, jako y_i, a średnią algebraiczną głosów dostarczonych przez te y_i, nagłówki dla węzła 0 jako b_i Niech macierz Y = diag[y₁….y_N-1] i wektor B = [b1…b_N-1]. A później aktualizacja reguły w Równaniu  zmienia się na

Jeśli wykres zaufania jest silnie powiązany, to znaczy C jest nieredukowalny, wektor zaufania zbiega się do unikalnego wektora zaufania z

T = (Z + Y – C)^-1YB

Wiarygodność węzła 0 jest funkcją liczby nagłówków i ich głosów. Aby zwiększyć swoje wartości zaufania, aby były powyżej progu η⁺, węzeł 0 musi uzyskać większe zaufanie z nagłówków. Co ciekawsze, schemat głosowania można interpretować jako łańcuch Markowa na ważonym, ukierunkowanym wykresie. Każdy węzeł jest stanem w łańcuchu Markowa z macierzą przejścia M; załóżmy, że rozważamy wartość zaufania t_i0, łańcuch Markowa zaczyna się od stanu i i wybiera następny stan zgodnie z macierzą przejścia. Zdefiniuj p^τ_ij jako prawdopodobieństwo, że łańcuch Markowa znajduje się w węźle j w czasie τ. Następnie tymczasowa wartość zaufania reprezentuje oczekiwaną wartość zaufania w bieżącym czasie, co jest prawdopodobieństwem, że łańcuch Markowa znajduje się w węźle j w czasie τ. Wówczas tymczasowa wartość zaufania reprezentuje oczekiwaną wartość zaufania w bieżącym czasie, czyli

Z macierzy przejść nagłówki w rzeczywistości absorbują stany w łańcuchu Markowa, które nie mają łącza wychodzącego. Następnie poprzedni wykres zaufania przedstawiony na rysunku wcześniejszym można zmodyfikować tak, aby przedstawiał ocenę węzła 0 jako łańcucha Markowa, jak pokazano na rysunku.

Łańcuch Markowa ostatecznie zatrzyma się w jednym z absorbujących stanów. Załóżmy, że prawdopodobieństwo zatrzymania się w nagłówku h zaczynając od i wynosi q_ih, a wartość zaufania h na węźle 0 wynosi v_h0. Następnie ostateczną wartość zaufania nadaje

Łańcuch Markowa można postrzegać jako przypadkowy spacer po dwuznakach. Załóżmy, że agent mobilny porusza się po digrafie zgodnie z macierzą przejścia. Jako następny przeskok wybiera sąsiada o wysokim prawdopodobieństwie przejścia. Prawdopodobieństwa przejścia zależą od wartości ufności. Dlatego agent mobilny ma tendencję do odwiedzania węzłów, które są silnie połączone i mają wysokie wartości ufności. Tak więc oczekiwane wartości zaufania mają większe znaczenie dla wysoce połączonych i wysoce zaufanych węzłów, które zwykle dostarczają stosunkowo dokładnych informacji.

Przedstawiamy prostą regułę oceny zwana prostą regułą głosowania do oceny wartości ufności. Załóżmy, że bezpośrednie wartości ufności są stałe, to znaczy za każdym razem τ ≥  0, c_it(τ) = c_ik, i nie zawsze jest to prawdą, ponieważ węzły zawsze są skłonne dostosować swoje opinie w oparciu o nowe informacje. Ta sekcja dotyczy konwergencji zasad oceny. Zmieniając wartości głosów, czas konwergencji będzie się różnił, ale ostatecznie wartość zaufania zbiegnie się do tego samego stanu ustalonego, biorąc pod uwagę, że opinie zostaną ostatecznie ustalone. t_ij(t) jest używane jako wartość zaufania i na j w czasie t .Wtedy

gdzie

ponieważ brane są pod uwagę tylko opinie sąsiadów o pozytywnym przekonaniu, i

W regule głosowania węzeł k, sąsiad i, głosuje na cel j z bieżącą wartością zaufania, jaką ma t_kj(τ – 1) Węzeł i łączy wszystkie te głosy za pomocą średniej ważonej, gdzie wagi są równe bezpośrednim wartościom ufności i dla jego sąsiadów. Zwróć uwagę, że obliczenie f, y jest niezależne od wartości zaufania w innych węzłach. Jedyne wartości, które mają znaczenie, to wartości zaufania dotyczące j i bezpośrednie wartości zaufania. Oceńmy zaufanie w konkretnym węźle, powiedzmy na węźle 0. Zdefiniujmy macierz (N – 1) x (N – 1), c⁺⁰ = {c_tj^*}, i, j = 1 … N-1 i wektor zaufania na 0 jako T⁽⁰⁾ = [t₁₀, t₂₀ … ,t_(N-i)0] – Następnie przepisuje się pierwsze równanie  w formacie macierzowym w następujący sposób:

gdzie:

Z(0) = diag [z₁, …, z_N-1].

Powyższe równanie działa również dla oceny w innych węzłach. Równanie można wykorzystać, pomijając indeks 0, jak poniżej:

Gdy τ stanie się duży, wektor zaufania zbiegnie się do stanu ustalonego, który decyduje o wartościach zaufania w celu. Niech t_i0 = lim_τ→∞ t_i0(τ), oznacza wartość zaufania i na 0 w stanie ustalonym. Wartości zaufania w stanie ustalonym nazywane są ostatecznymi wartościami zaufania, a te w dowolnym momencie przed konwergencją nazywane są tymczasowymi wartościami zaufania. Do ostatecznych wartości zaufania stosuje się regułę progową. Reguła progowa jest definiowana za pomocą parametrów η^– i  η⁺ w taki sposób, że wartość zaufania jest neutralna między η^– i  η⁺, podczas gdy warunek zaufania przeważa, gdy 1> wartość zaufania >  η⁺, a warunek braku zaufania występuje, gdy η^–   < wartość zaufania <-1.

Nieufność jest zwykle ignorowana w większości prac nad zarządzaniem zaufaniem. Jednak prawdziwy świat uważa, że ​​nieufność jest co najmniej tak samo ważna jak zaufanie. W przypadku sieci z adwersarzami systemy powinny zwracać jeszcze większą uwagę na informacje o nieufności niż na informacjach o zaufaniu, ponieważ szkody wyrządzane przez adwersarzy są zwykle tak poważne, że sieć może zostać całkowicie zamknięta. Wobec braku nieufności nie jest jasne, czy wartość zaufania równa 0 oznacza nieufność, czy „brak opinii”. Jiang i Baras  wyraźnie ustalili wartości zaufania między -1 a 1, mając nieufność oznaczoną jako -1 i „brak opinii” jako 0. Modelowanie nieufności jako negatywnego zaufania wiąże się z kilkoma wyzwaniami, na przykład, jeśli konieczne jest połączenie nieufności w łańcuchu zaufania. Guha podali trzy modele propagowania zaufania i nieufności: tylko zaufanie, gdzie nieufność jest całkowicie ignorowana; jednoetapowa nieufność, gdzie kiedy nie ufam j, nie ufam wszystkim opiniom j, a zatem nieufność propaguje tylko jeden krok; i propaguje nieufność, gdy zaufanie i nieufność rozprzestrzeniają się razem. Wyniki eksperymentów wykazały, że jednoetapowa propagacja nieufności działa lepiej w porównaniu z innymi. Dlatego ten model wykresu obejmuje również nieufność za pomocą jednostopniowego modelu nieufności. Zatem jeśli c_ij <0, nie będę prosić j o opinię, podczas gdy zaufanie negatywne mam na j wpływa na zaufanie innych oszacowań na j. Następnie ogólna zasada oceny podana w równaniu powyżej została zmodyfikowana, aby uwzględnić nieufność w następujący sposób:

Rozumie się, że jeśli t_kj wypadnie negatywnie, oznacza to nieufną opinię.

Nieufność jest zwykle ignorowana w większości prac nad zarządzaniem zaufaniem. Jednak prawdziwy świat uważa, że ​​nieufność jest co najmniej tak samo ważna jak zaufanie. W przypadku sieci z adwersarzami systemy powinny zwracać jeszcze większą uwagę na informacje o nieufności niż na informacjach o zaufaniu, ponieważ szkody wyrządzane przez adwersarzy są zwykle tak poważne, że sieć może zostać całkowicie zamknięta. Wobec braku nieufności nie jest jasne, czy wartość zaufania równa 0 oznacza nieufność, czy „brak opinii”. Jiang i Baras  wyraźnie ustalili wartości zaufania między -1 a 1, mając nieufność oznaczoną jako -1 i „brak opinii” jako 0. Modelowanie nieufności jako negatywnego zaufania wiąże się z kilkoma wyzwaniami, na przykład, jeśli konieczne jest połączenie nieufności w łańcuchu zaufania. Guha podali trzy modele propagowania zaufania i nieufności: tylko zaufanie, gdzie nieufność jest całkowicie ignorowana; jednoetapowa nieufność, gdzie kiedy nie ufam j, nie ufam wszystkim opiniom j, a zatem nieufność propaguje tylko jeden krok; i propaguje nieufność, gdy zaufanie i nieufność rozprzestrzeniają się razem. Wyniki eksperymentów wykazały, że jednoetapowa propagacja nieufności działa lepiej w porównaniu z innymi. Dlatego ten model wykresu obejmuje również nieufność za pomocą jednostopniowego modelu nieufności. Zatem jeśli c_ij <0, nie będę prosić j o opinię, podczas gdy zaufanie negatywne mam na j wpływa na zaufanie innych oszacowań na j. Następnie ogólna zasada oceny podana w równaniu powyżej została zmodyfikowana, aby uwzględnić nieufność w następujący sposób:

Rozumie się, że jeśli t_kj wypadnie negatywnie, oznacza to nieufną opinię.

Szacowanie zaufania w sieciach o ograniczonych zasobach, takich jak mobilne sieci ad hoc (MANET), sieci czujników, samochodowe sieci ad hoc (VANET) i wszechobecne systemy komputerowe, jest znacznie bardziej złożone niż w tradycyjnych sieciach, takich jak Internet i bezprzewodowe sieci LAN ze stacjami bazowymi i punkty dostępu. Sieci autonomiczne, które nie mają ani wcześniej ustalonej infrastruktury, ani scentralizowanych serwerów sterujących, zależą od swoich rówieśników, z którymi tworzą sieć. Istotne cechy rozproszonego zarządzania zaufaniem w MANET-ach względem sieci tradycyjnych i scentralizowanych są wymienione poniżej:

• Niepewność i niekompletność. Wartość zaufania mieści się w zakresie od -1 do 1, gdzie -1 oznacza całkowitą nieufność, a 1 oznacza pełne zaufanie. Zaufane dowody są dostarczane przez rówieśników, które mogą być niekompletne, a nawet nieprawidłowe.
• Lokalność. Informacje o zaufaniu koncentrują się lokalnie. Globalna wymiana wartości zaufania wymaga wysokich kosztów komunikacji, ponieważ szybkie zmiany w sieci prowadzą do częstych aktualizacji wartości zaufania.
• Obliczenia rozproszone. Każdy węzeł przeprowadza ocenę zaufania niezależnie.

Jednak rozproszone obliczenia zaufania mają kilka zalet. Właściwość Lokalność oszczędza zasoby sieciowe, takie jak moc, przepustowość, obliczenia i pamięć. Pozwala to również uniknąć pojedynczego punktu awarii. Ponadto sieci autonomiczne są dynamiczne z częstymi zmianami topologii i członkostwa, a rozproszone obliczenia zaufania obejmują kontakt tylko z kilkoma łatwo dostępnymi węzłami. Innymi słowy, ocena zaufania ogranicza się do informacji dostarczanych przez bezpośrednio połączone węzły, to znaczy opiera się na lokalnych interakcjach. Pośrednie relacje między dwoma podmiotami, które wcześniej nie wchodziły w interakcję, są realizowane przy użyciu bezpośrednich relacji zaufania, które mają ze sobą węzły pośrednie. Kilka prac badawczych dotyczących obliczania zaufania opiera się na relacjach z sąsiadami z jednym przeskokiem. Bezpośrednie obserwacje są wymieniane między sąsiednimi węzłami. Załóżmy, że węzeł A otrzymuje opinie swoich sąsiadów na temat węzła X w sieci. Węzeł A łączy opinie swoich sąsiadów, jeśli są one bliskie opinii A w tym węźle. W artykule przedstawiono metodę powiązania wiarygodności węzłów z jakością dostarczanych przez nie danych. Jiang i Baras badają wnioskowanie o wartości zaufania, a nie o generowaniu bezpośredniego zaufania, wykorzystując wartości Eigen Trust wprowadzone przez Kamvara . W Eigen Trust opinie sąsiadów są ważone przez zaufanie, jakim obdarzają ich:

gdzie:t_ik oznacza lokalną wartość zaufania i obliczoną dla węzła k od sąsiadów j  Wartości zaufania są znormalizowane, aby spełnić S; c, y = 1. Aby rozwiązać problem zmowy adwersarzy, zakładają, że w sieci są rówieśnicy, którym można wstępnie zaufać. Podobne algorytmy oceniają zaufanie poprzez łączenie opinii wybranej grupy użytkowników. Jednym możliwym wyborem dla wybranych użytkowników są sąsiedzi typu one-hop. Oprócz powyższych prac, obszerne badania skupiły się na projektowaniu zdecentralizowanych protokołów zaufania. Formalnie wszystkie te protokoły kategoryzują informacje o zaufaniu jako bezpośrednie zaufanie i zalecenia i są oceniane poprzez agregowanie opinii zaufania wzdłuż określonej ścieżki. Jiang i Baras sformułowali regułę interakcji lokalnej przy użyciu teorii grafów algebraicznych i przedstawili teoretyczne uzasadnienie zarządzania siecią, które ułatwia propagację zaufania. Model wykorzystuje bezpośrednie połączenia zaufania między węzłami jako skierowany graf (dwuznak) G (V,E), zwany grafem zaufania. Węzły wykresu to użytkownicy / podmioty w sieci. Załóżmy, że liczba węzłów w sieci wynosi N, to znaczy |V| = N, a węzły są oznaczone indeksami [0,1 ,. . ., N – 1}. Skierowany łuk od węzła i do węzła j, oznaczony jako (i, j), odpowiada relacji zaufania, jaką podmiot I, nazywany również powiernikiem, ma z podmiotem j, zwanym również powiernikiem. Każdy łuk ma również wagę zwaną wartością ufności. Funkcja wagi np.

VxV → W, gdzie W = [-1,1] reprezentuje stopień przekonania i na j. W digrafie, łuki łączące dwa węzły w tym samym kierunku nazywane są łukami równoległymi, a pętla to łuk, który łączy węzeł ze sobą. Załóżmy, że wykres zaufania jest prostym wykresem bez równoległych łuków lub pętli, ponieważ uważa się, że relacja zaufania znajduje się między dwiema odrębnymi jednostkami i jest wyjątkowa w danym kontekście. Zbiór sąsiadów dla węzła i jest określony przez następujące równanie:

Rysunek

ilustruje przykład wykresu zaufania. W przypadku jednorodnej sieci rozproszonej wszystkie węzły są traktowane równo. Jeśli węzeł i chce oszacować wiarygodność węzła j, wymagane jest zagregowanie wszystkich opinii jego sąsiadów na temat j, czyli relacji zaufania, jakie sąsiedzi mają względem j. Można to interpretować jako następującą ogólną zasadę:

Obowiązkowa zasada jest taka, że nie bierzemy pod uwagę opinii samego węzła docelowego. Funkcja f(.) Powinna spełniać następujące właściwości:

• Węzły ufają sobie, to znaczy t_ti = 1.
• —1 ≤ f(.) ≤ 1, ponieważ nasza wartość zaufania mieści się w zakresie od -1 do1.
• Opinie węzłów o wysokich wartościach ufności są bardziej realistyczne, więc powinny mieć większą wagę.

Topologia będzie się różnić, ponieważ niektóre węzły będą wchodzić i wychodzić z zasięgu sieci bezprzewodowej. Dlatego liczba przeskoków między źródłem a miejscem docelowym również będzie się różnić. Przepustowość sieci również będzie się zmieniać, ponieważ im większa liczba przeskoków, tym większe będzie opóźnienie routingu. Gdy odległość między węzłami bezprzewodowymi wzrasta, stosunek sygnału do szumu (SNR) maleje, a osiągalna przepustowość zostaje zmniejszona. Problemy z trasowaniem dzielą się na dwie kategorie: wykrywanie tras i konserwacja tras. Routing można również podzielić na dwa różne modele: routing proaktywny, w którym tablice routingu we wszystkich węzłach są stale aktualizowane; reaktywny routing, w którym tabele routingu są aktualizowane tylko na żądanie. Routing proaktywny powinien być używany, gdy mobilność węzła jest niska, a ruch w sieci usługowej wymaga czasu rzeczywistego. Routing reaktywny jest używany, gdy zapotrzebowanie na transmisję w czasie rzeczywistym jest niskie. Wykrywanie tras jest przeprowadzane tylko wtedy, gdy potrzebna jest nowa trasa lub gdy stara trasa nie jest już sprawna. Kolejnym wyzwaniem technicznym jest skalowalność.

Gupta i Kumar pokazali bardzo interesujący wynik oparty na prostym modelu interferencji. Jeśli istnieje N węzłów w ograniczonym regionie, całkowita przepustowość sieci bezprzewodowej ad hoc rośnie przy √N, co oznacza, że ​​przepustowość na węzeł spada o 1/√N. Dlatego przy dużej liczbie węzłów wydajność na węzeł zbliża się do zera. Liczba aktualizacji tras również wzrośnie wraz z liczbą węzłów. Jest to oczywiście problem ze skalowaniem. Trzecim wyzwaniem jest zasilanie węzłów mobilnych za pomocą baterii. Przesyłanie pakietów w celu aktualizacji tras lub pakietów innych węzłów może kusić użytkowników do wyłączenia sprzętu i włączenia go tylko wtedy, gdy chcą się komunikować. Rozwiązaniem, które wydłuża żywotność baterii, jest produkcja lepszych baterii, dostosowanie mocy nadajnika do długości ścieżki bezprzewodowej oraz przełączenie sprzętu w tryb uśpienia, gdy nie ma ruchu. Najpoważniejszym wyzwaniem jest bezpieczeństwo. W niektórych pracach znalezionych w literaturze podjęto próbę zabezpieczenia bezprzewodowych sieci ad hoc jako głównego tematu. Wszystkie opisują zasady i metody dodawania zabezpieczeń do istniejących protokołów routingu ad hoc, gdzie bezpieczeństwo nie było problemem od samego początku. Obecnie bardzo ograniczającym czynnikiem jest pojemność terminali. Gdy N terminali, z których każdy ma pojemność C, ściśle ze sobą współpracuje, tworząc sieć ad hoc, użyteczna pojemność CU każdego terminalu (z powodu zakłóceń) to CU = C /√N. Ze 100 zaciskami w sieci, użyteczna pojemność każdego terminala będzie wynosić tylko 10% jego pierwotnej pojemności. Protokół routingu może wykorzystywać 70% -80% tej przepustowości, jeśli terminale są bardzo mobilne. Aby sieć ad hoc była bezpieczna, konieczna jest pewna forma uwierzytelnienia, która z łatwością może wykorzystać resztę przepustowości, zwłaszcza jeśli jest oparta na infrastrukturze klucza publicznego i kryptografii progowej. Bezpieczeństwo w samoorganizujących się sieciach charakteryzuje dostępność, integralność, poufność, autentyczność i odpowiedzialność. Podstawowym wyzwaniem związanym z utrzymaniem bezpieczeństwa i niezawodności samoorganizujących się sieci jest obsługa zaufania oraz posiadanie wydajnych i działających mechanizmów bezpieczeństwa i sieci w ciągle zmieniających się warunkach w sieciach ad hoc, w których węzły przemieszczają się swobodnie; komunikować się między sobą za pomocą podatnej na błędy komunikacji bezprzewodowej multihop; i może dynamicznie dołączyć, opuścić lub przegrać.