Teraz rozważamy więcej niż jednego, powiedzmy M, przeciwników jest obecnych w sieci. Zgodnie z założeniami przeciwnicy ci znają się nawzajem i potrafią zmowy, aby maksymalnie zniszczyć schemat głosowania. Podobnie, jak w powyższym argumencie, najgorszą strategią tych przeciwników M jest zawsze głosowanie – 1 na dobre węzły i odwrotnie 1 na innych przeciwników i nigdy nie zmieniają swoich głosów. Zatem w dwuznakach przeciwnicy są modelowani jako stany absorbujące. Załóżmy, że system ocenia dobry węzeł, powiedzmy 0. Załóżmy, że istnieją nagłówki H, a ich głosy w węźle 0 są oznaczone przez vh0 dla dowolnego nagłówka h. Jeśli przyjmiemy, że wykres zaufania jest idealnie regularny w tym sensie, że prawdopodobieństwa absorpcji nagłówków i przeciwników są takie same i są oznaczone jako q , a następnie q(H + M) = 1. Wartość zaufania określa następujące równanie:
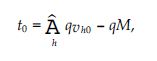
co jest takie samo dla wszystkich węzłów oceniających. Następnie należy oszacować wpływ na bezpieczeństwo jako funkcję liczby przeciwników. Zgodnie z regułą progową, węzeł 0 nie jest zaufany, jeśli t < η+ i mamy q(Shvho -M) < h+.
Zatem jeśli liczba przeciwników M > (Shvho – h*H)/(1+h+) = M* schemat nie jest w stanie ocenić wiarygodności węzła 0. Dlatego M* jest progiem odporności na atak dla schematu głosowania. W bardziej realistycznym scenariuszu jednostki o niskich wartościach ufności są łatwe do oszukania przez przeciwników. Adwersarze, którzy łączą się z podmiotami o niskim zaufaniu, mają mniejsze prawdopodobieństwo absorpcji, wtedy próg odporności na atak jest w rzeczywistości większy niż M*, co oznacza, że schemat jest odporny na więcej przeciwników. Argumenty dotyczące wykrywania przeciwników są podobne do oceny, z tym wyjątkiem, że liczba przeciwników jako stanów absorbujących wynosi (M – 1) zamiast M, ponieważ przeciwnik M-ty jest teraz celem oceny. W tej sekcji formalnie zdefiniowano strategię ustanawiania zaufania opartą wyłącznie na lokalnych interakcjach. Wprowadził również nowe pojęcie nagłówków, które pomagają w tworzeniu rozproszonego zaufania. Zachowanie zbieżności schematu wykorzystującego teorię grafów algebraicznych jest badane i interpretowane jako łańcuch Markowa na dwuznaku. Ponadto omówiono wpływ topologii na rozprzestrzenianie zaufania, co wyjaśnia nowy sposób zarządzania siecią. Ponieważ zarządzanie zaufaniem jest ważnym elementem bezpieczeństwa sieci, badane są kwestie dotyczące ustanowienia zaufania w obecności adwersarzy.