Aby ocenić dany węzeł, opinie o zaufaniu rozpoczynają się od węzłów, które mają bezpośrednie relacje zaufania z celem. Opinie te rozprzestrzeniają się po całej sieci i ostatecznie docierają do wszystkich węzłów w sieci. Rozważmy teraz konwergencję systemu, a także zbadajmy rozprzestrzenianie się zaufania, gdy system osiąga stan ustalony. Rozważmy sieć cnotliwą bez przeciwników, w której wszystkie węzły zachowują się racjonalnie, to znaczy wszystkie węzły stosują się do wstępnie zaprojektowanej reguły oceny, a ten przypadek skutkuje C+ = C. Analiza przedstawiona poniżej pokazuje, że zaufania nie można ustanowić za pomocą prostej reguły głosowania. Zdefiniuj macierz M = Z-1C. Następnie równanie 8.6 aktualizacji stanu można zapisać w następujący sposób:
T(t) = MT(t-1) = MTT(0)
M można postrzegać jako ważoną macierz sąsiedztwa wykresu zaufania. Konieczne jest sprawdzenie, czy M jest matrycą stochastyczną. Macierz nazywana jest macierzą stochastyczną, jeśli suma elementów każdego wiersza wynosi 1. Ponieważ M jest macierzą stochastyczną, największa wartość własna Mis 1. Mówi się, że graf zaufania jest silnie połączony, jeśli do każdego węzła można dotrzeć z każdego innego węzła podążającego za kierunkiem krawędzi. Można wykazać, że wykres, którego (ważona) macierz sąsiedztwa jest M, jest silnie powiązany wtedy i tylko wtedy, gdy macierz jest błędnie nieredukowalna. Niech wektor wierszowy π będzie lewym wektorem własnym (wektorem wierszowym) odpowiadającym wartości własnej 1 z |π| = 1, a następnie πM = π. Można to udowodnić przez ergodyczność, która mówi
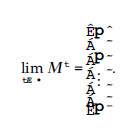
Zatem i, 1 ≤ i ≤ N -1
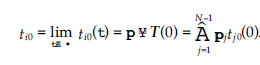
Ponieważ ti0 jest niezależne od i, każdy węzeł osiąga tę samą wartość zaufania w stanie ustalonym. Jak widać, wartości zaufania zależą wyłącznie od początkowego wektora zaufania T (0). Jeśli węzeł jest na początku zaufany przez dużą część węzłów w sieci, jego wartości zaufania są wysokie w stanie ustalonym. Jednak w sieciach rozproszonych początkowo tylko niewielka liczba węzłów ma bezpośrednie relacje zaufania z celem, to znaczy T (0) jest rzadki i zawiera kilka niezerowych wpisów. Ponadto wpisy n są zwykle małe, gdy N jest duże. Na przykład rozważmy wykres regularny / c, na którym wszystkie łuki mają wartość ufności 1. Następnie lewy wektor własny p = [1 /(N -1), …, 1 /N -1)]¢ Ponieważ wykres zaufania jest rzadki, k << N, mamy
ti0 = k /N – 1 << 1
Wynik wskazuje, że nawet w sieci, w której wartości ufności wszystkich sąsiadów są równe 1, wartości zaufania w stanie ustalonym są bardzo małe, to znaczy bliskie 0. W związku z tym, zgodnie z prostą regułą głosowania, ustanowienie zaufania jest prawie niemożliwe, nawet jeśli wszystkie wartości głosów to 1. W celu przezwyciężenia tego problemu wprowadza się nagłówki, które są wstępnie zaufanymi podmiotami o wartości zaufania 1. Jednostkę można uznać za nagłówek tylko wtedy, gdy udowodniono, że jest niezawodna i odporna na ataki. Zdefiniujmy liczbę nagłówków i, którym ufam, jako yi, a średnią algebraiczną głosów dostarczonych przez te yi, nagłówki dla węzła 0 jako bi Niech macierz Y = diag[y1….yN-1] i wektor B = [b1…bN-1]. A później aktualizacja reguły w Równaniu zmienia się na
![]()
Jeśli wykres zaufania jest silnie powiązany, to znaczy C jest nieredukowalny, wektor zaufania zbiega się do unikalnego wektora zaufania z
T = (Z + Y – C)-1YB
Wiarygodność węzła 0 jest funkcją liczby nagłówków i ich głosów. Aby zwiększyć swoje wartości zaufania, aby były powyżej progu η+, węzeł 0 musi uzyskać większe zaufanie z nagłówków. Co ciekawsze, schemat głosowania można interpretować jako łańcuch Markowa na ważonym, ukierunkowanym wykresie. Każdy węzeł jest stanem w łańcuchu Markowa z macierzą przejścia M; załóżmy, że rozważamy wartość zaufania ti0, łańcuch Markowa zaczyna się od stanu i i wybiera następny stan zgodnie z macierzą przejścia. Zdefiniuj pτij jako prawdopodobieństwo, że łańcuch Markowa znajduje się w węźle j w czasie τ. Następnie tymczasowa wartość zaufania reprezentuje oczekiwaną wartość zaufania w bieżącym czasie, co jest prawdopodobieństwem, że łańcuch Markowa znajduje się w węźle j w czasie τ. Wówczas tymczasowa wartość zaufania reprezentuje oczekiwaną wartość zaufania w bieżącym czasie, czyli
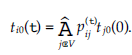
Z macierzy przejść nagłówki w rzeczywistości absorbują stany w łańcuchu Markowa, które nie mają łącza wychodzącego. Następnie poprzedni wykres zaufania przedstawiony na rysunku wcześniejszym można zmodyfikować tak, aby przedstawiał ocenę węzła 0 jako łańcucha Markowa, jak pokazano na rysunku.
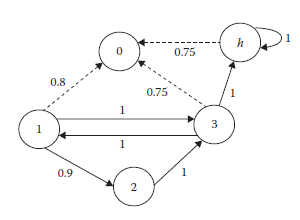
Łańcuch Markowa ostatecznie zatrzyma się w jednym z absorbujących stanów. Załóżmy, że prawdopodobieństwo zatrzymania się w nagłówku h zaczynając od i wynosi qih, a wartość zaufania h na węźle 0 wynosi vh0. Następnie ostateczną wartość zaufania nadaje
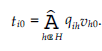
Łańcuch Markowa można postrzegać jako przypadkowy spacer po dwuznakach. Załóżmy, że agent mobilny porusza się po digrafie zgodnie z macierzą przejścia. Jako następny przeskok wybiera sąsiada o wysokim prawdopodobieństwie przejścia. Prawdopodobieństwa przejścia zależą od wartości ufności. Dlatego agent mobilny ma tendencję do odwiedzania węzłów, które są silnie połączone i mają wysokie wartości ufności. Tak więc oczekiwane wartości zaufania mają większe znaczenie dla wysoce połączonych i wysoce zaufanych węzłów, które zwykle dostarczają stosunkowo dokładnych informacji.