Becker i Willie zaproponowali protokół Octopus (BW) do obliczania kluczy grupowych. Niech G będzie grupą cykliczną rzędu q a α będzie generatorem G. Protokół zakłada istnienie bijekcji Φ: G → Zq. Uczestnicy są podzieleni na cztery grupy: I(A), I(B), I(C) i I(D) z A, B, C i D jako liderami grup. A przeprowadza wymianę klucza DH z każdym członkiem grupy P(i), w wyniku czego powstaje klucz k(i), gdzie P(i) Є I (A). A oblicza klucz K(A) = Πiφ [k(i)]. B, C i D wykonują tę samą sekwencję kroków co A. A dokonuje wymiany klucza DH z B, w wyniku czego powstaje klucz αK[I(A)UI(B)]. Podobnie C dokonuje wymiany kluczy DH z D. Klucz grupy jest obliczany
w następujący sposób:
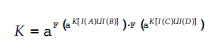
A wysyła αK[I(A)UI(B) i αK[I(A)UI(B)] do P (j) Є I (A), aby P (j) mógł obliczyć K. zakłada się, że każdy lider grupy używa różnych kluczy krótkoterminowych do wymiany DH z każdym członkiem grupy w celu obliczenia klucza k (j). W takim przypadku, jeśli intruz zna krótkoterminowe klucze członka grupy, powiedzmy IA, z prawdopodobieństwem p, to zakładając, że jest ich (n – 4) / 4, prawdopodobieństwo poznania kluczy wszystkich członków jest p(n−4)/4. Wystarczy znać klucz I(A) lub I(B) lub I(C) lub I(D), aby poznać klucz sesji. Dlatego prawdopodobieństwo, że intruz zna klucz sesji i DPFS, wynosi 1− (1 – p(n−4)/4)4. Można wywnioskować, że w tym protokole wiadomo, że klucze wszystkich członków podgrupy naruszają klucz sesyjny. W takim protokole możliwe są złośliwe ataki grupowe.